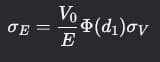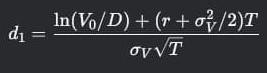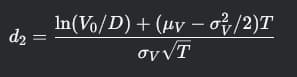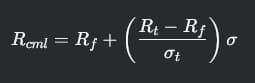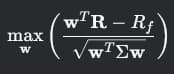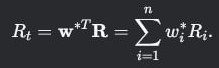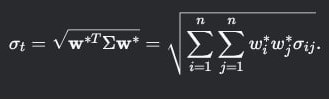📊 Портфель Марковица

Портфель Марковица - финансовая модель, которая находит оптимальный баланс между желаемой доходностью и допустимым уровнем риска.

В рамках теории Марковица можно выделить две основные оптимизационные задачи, которые решаются для построения Эффективной Границы. Обе они математически эквивалентны и приводят к одному и тому же множеству оптимальных портфелей, но формулируются с разных точек зрения, удобных для разных типов инвесторов:

1. Задача Минимизации Риска при Заданной Ожидаемой Доходности:

Этот подход предпочитает инвестор, который знает, какой уровень доходности ему нужен (например, чтобы достичь финансовой цели), и хочет достичь этой цели с наименьшими колебаниями стоимости своего портфеля. Он фокусируется на защите капитала при достижении конкретной цели.

Считается путем выражения в виде Лагранжиана:

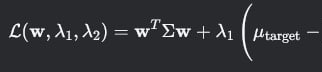
Далее берутся частные производные по ω, λ1 и λ2 и приравниваются к 0, после получается система, из которой получаем доли активов и итоговый риск:

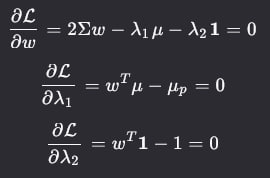
2. Задача Максимизации Доходности при Заданном Уровне Риска:

Этот подход предпочитает инвестор, который знает, какой уровень риска (волатильности) он психологически и финансово готов вынести. Он хочет "выжать максимум" из своего допустимого риска. Он фокусируется на росте капитала в рамках своих ограничений по риску.

Считается путем выражения в виде Лагранжиана:

Принцип такой же, как и у первой задачи. Как итог получаем веса активов и итоговую доходность

🏢 Модель Мертона

Модель Мертона оценивает ненаблюдаемые параметры — стоимость активов компании (V) и их волатильность (σₐ) — через рыночные данные об акциях (капитализацию E и волатильность акций σₑ) и балансовый долг (D).

Это решается через систему двух уравнений, основанных на аналогии с опционом колл:

где:

E - капитализация компании
D - долг компании
σe - волатильность всех активов
σv - волатильность акций

Также используется нормализация переменных d1 и d2:

На этом сайте модель Мертона используется расчет ожидаемой доходности с учетом характеристик компании, выпускающей акции.

Сама доходность расчитывается по следующей формуле:

где:

r - безрисковая ставка
Δleverage - дельта-рычаг. Рассчитывается по формуле:

μv - доходность акций без учета характеристик компании. Рассчитывается через CAPM

📈 CML (Capital Market Line)

CML — это ключевая концепция современной портфельной теории (Modern Portfolio Theory, MPT), которая показывает зависимость между ожидаемой доходностью и риском эффективных портфелей, включающих безрисковый актив и тангенсный портфель.

Расчитывается по формуле:

где:

E(Rp) — ожидаемая доходность портфеля
Rf — безрисковая ставка (например, доходность ОФЗ)
E(Rm) — ожидаемая доходность тангенсного портфеля
σm — стандартное отклонение (риск) тангенсного портфеля.
σp — стандартное отклонение (риск) рассматриваемого портфеля.

🎯 Тангенсный портфель

Портфель с максимальным углом наклона (Sharpe Ratio): Прямая CML имеет максимально возможный наклон среди всех линий, соединяющих Rf с любой точкой на эффективной границе или внутри нее. Этот наклон — это коэффициент Шарпа (Sharpe Ratio) самого тангенсного портфеля. Таким образом, T — это портфель с максимально возможным коэффициентом Шарпа (избыточная доходность на единицу риска) на рынке.

Таким образом, тангенсный портфель рассчитывается путем максимизации коэффициента Шарпа:

где:

σij - ковариация между активами
w - веса активов
Rt - доходность тангенсного портфеля
σt - риск тангенсного портфеля

💰 CAPM (Capital Asset Pricing Model)

CAPM (Capital Asset Pricing Model) — это финансовая модель, которая связывает ожидаемую доходность актива с его риском по отношению к рынку.

где:

E(Ri) — ожидаемая доходность актива,
Rf — безрисковая ставка,
βi — бета-коэффициент, мера риска актива относительно рынка,
E(Rm) — ожидаемая доходность индекса Мосбиржи

⚠️ Риск

Стандартное отклонение актива. Рассчитывается как корень из дисперсии:

📐 Бета-коэффициент

Бета акции (β) — это коэффициент, который показывает, насколько изменчива цена акции по сравнению с рынком в целом. Он используется в финансовом анализе для оценки рыночного риска.

β = 1 — Акция движется в точности как рынок.
β > 1 — Акция более волатильна, чем рынок (например, β = 1,5 означает, что если рынок растёт на 10%, акция может вырасти на 15%, и наоборот).
β < 1 — Акция менее волатильна, чем рынок (например, β = 0,7 означает, что при росте рынка на 10% акция вырастет только на 7%).
β < 0 — Акция движется в противоположном направлении от рынка (редкий случай).

Считается по формуле:

где:

Ri — историческая доходность акции
Rm — историческая доходность рынка

⭐ Коэффициент Шарпа

Коэффициент Шарпа — это показатель, который измеряет эффективность инвестиций с учётом риска.

> 1 — хорошая доходность с учетом риска,
> 2 — отличный результат,
< 1 — доходность не компенсирует риск,
Отрицательный — доходность ниже безрисковой ставки (плохо).

Считается по формуле:

Где:

Rp — средняя доходность портфеля (или актива),
Rf — безрисковая ставка,
σp — стандартное отклонение доходности портфеля (волатильность, мера риска).

📚 Математические формулы

📊 Портфель Марковица

1. Задача Минимизации Риска при Заданной Ожидаемой Доходности:

2. Задача Максимизации Доходности при Заданном Уровне Риска:

🏢 Модель Мертона

📈 CML (Capital Market Line)

🎯 Тангенсный портфель

💰 CAPM (Capital Asset Pricing Model)

⚠️ Риск

📐 Бета-коэффициент

⭐ Коэффициент Шарпа